√99以上 ルートの問題 中3 566830

中学数学 平方根 のコツ 平方根の近似値 式の値

 なぜなら、ルートの中が正の場合は、正の 乗根は必ず一つだけ存在するため、それを で表しています（そう定義できます）。 例えば、 の場合、2乗して3になる数は、1732と、1732の2つありますが、その中で 正実数 をであるものは一つだけです3・・・what did the tree say to the peo

ルートの問題 中3

ルートの問題 中3- ルートの問題です 計算せよ。(計算して簡単にせよ) と言う問題です 1√(1/5−1/4)^2 ()は全てルートの中です 2√(3−π)^2−√(−3)^2 こちらも同じです よろしくお願いします。 ルートの計算（基礎） 中3数学 ルートは2乗がポイントとなります。 2乗のものはルートの外に出さないといけません。 最初は素因数分解でいいですが、いずれはそれをしなくてもすぐにルートを簡単にできるよう、覚えるまで問題を解き

中学３年生 数学 計算たしかめミックス 練習問題 式の展開と因数分解 平方根 ２次方程式 ちびむすドリル 中学生

中学生の勉強方法 編集スタッフ01 中3数学平方根の練習問題にチャレンジ！(解説あり) こんにちは、あすなろスタッフのカワイです。 今回は平方根の問題演習です。 全部解くことが出来たら、この単元を十分理解していると言っても過言ではありません！中学3年生 数学 計算たしかめミックス 練習問題「式の展開と因数分解」「平方根」「2次方程式」 中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 中学3年生 数学 平方根の乗法・除法 問題プリント 無料ダウンロード 中3数学：平方根の計算の仕方を極めよう！ 掛け算・割り算も いつの間にか梅雨入りしていましたね。 梅雨といえば平方根！ （謎） 今日は平方根の計算の仕方、掛け算や割り算の問題について説明します。 平方根をマスターして、「世界のヘイホー

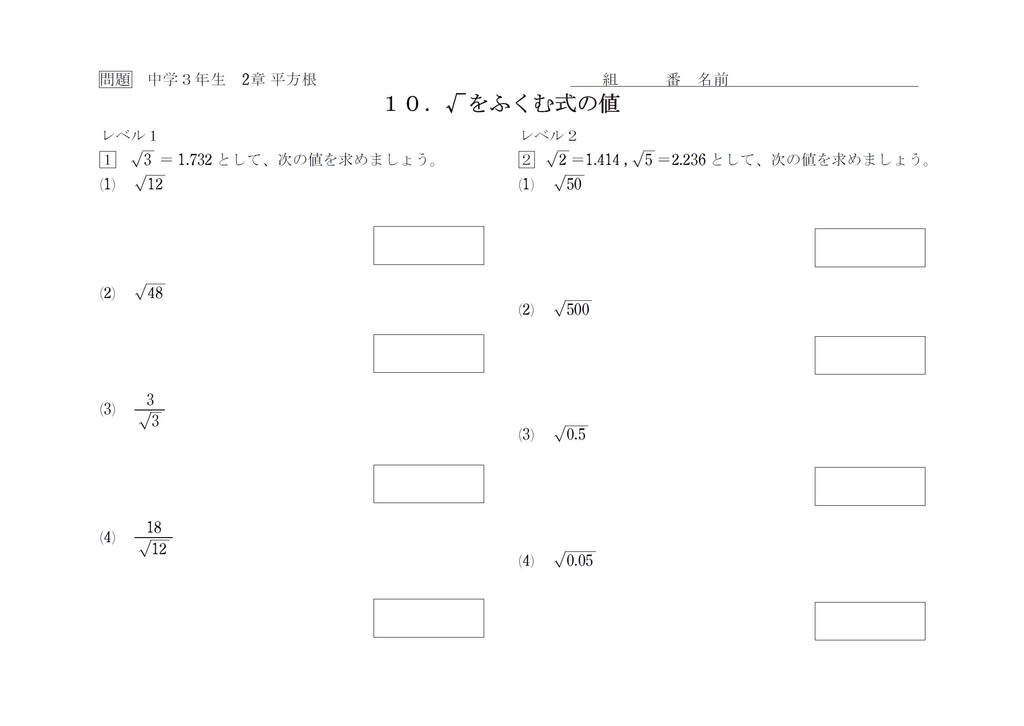
中3数学「二次方程式の解き方と因数分解」解の公式の覚え方と簡単な計算問題 今回は 中学3年の数学で学習する、因数分解や解の公式を利用した、二次方程式の解き方 についてお話しようと思います。 これを見れば、基本パターンはすべて網羅できる中3です。「平方根の近似値」、応用問題が。 中学生から、こんなご質問が届きました。 「 √の中が小数になっている時 の、 近似値の求め方が分かりません」 中3数学 三平方の定理（ピタゴラスの定理）の計算問題 の3つの解き方 中3数学 1 代入前に整えろ！式の値を求める応用問題の解き方 中3数学 3分でわかる！円周角の定理の逆の証明 中3数学

ルートの問題 中3のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	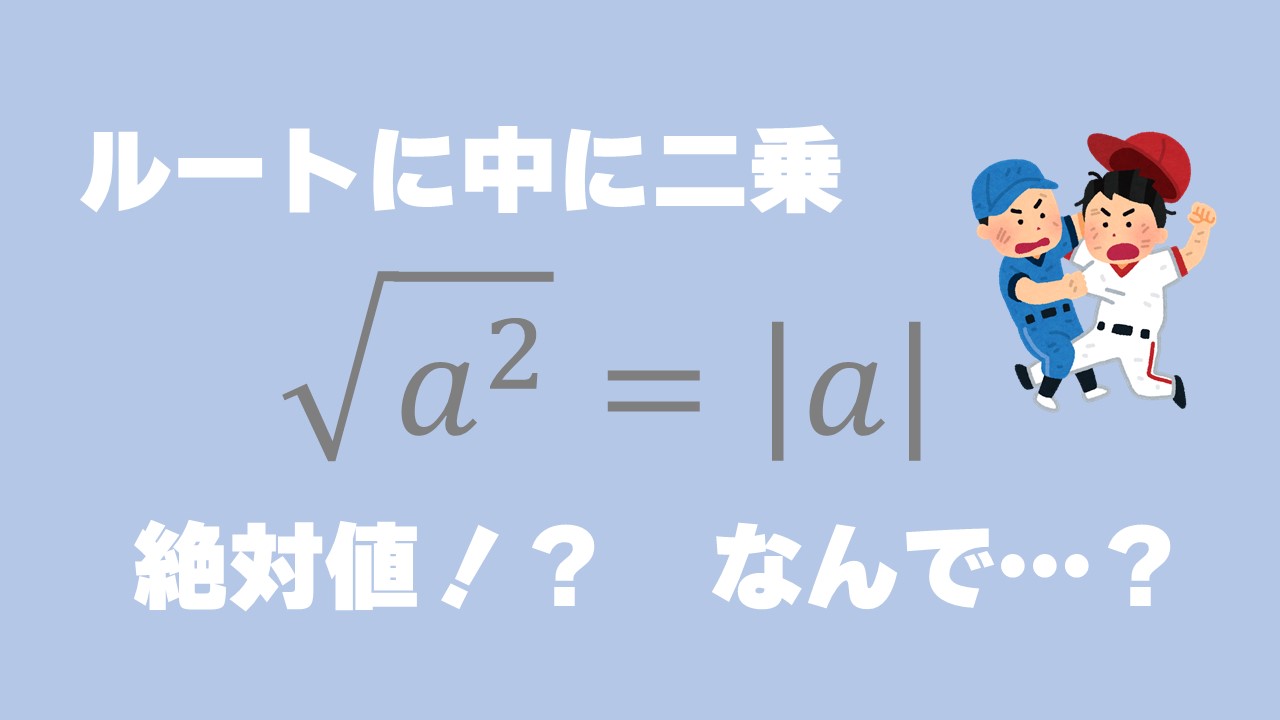中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	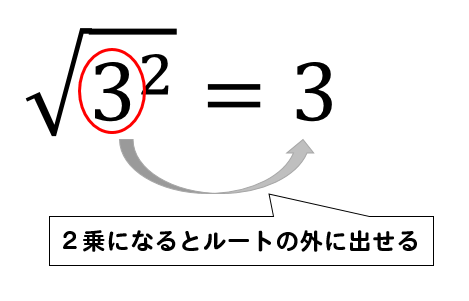中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
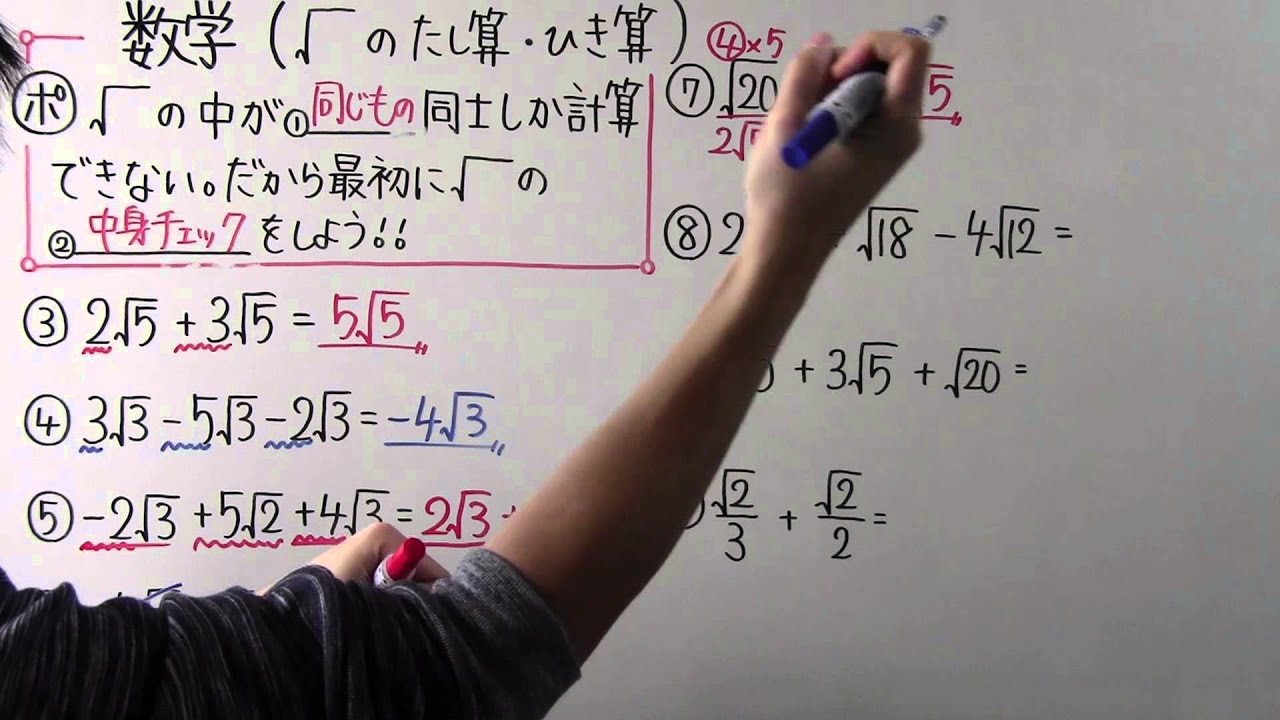中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	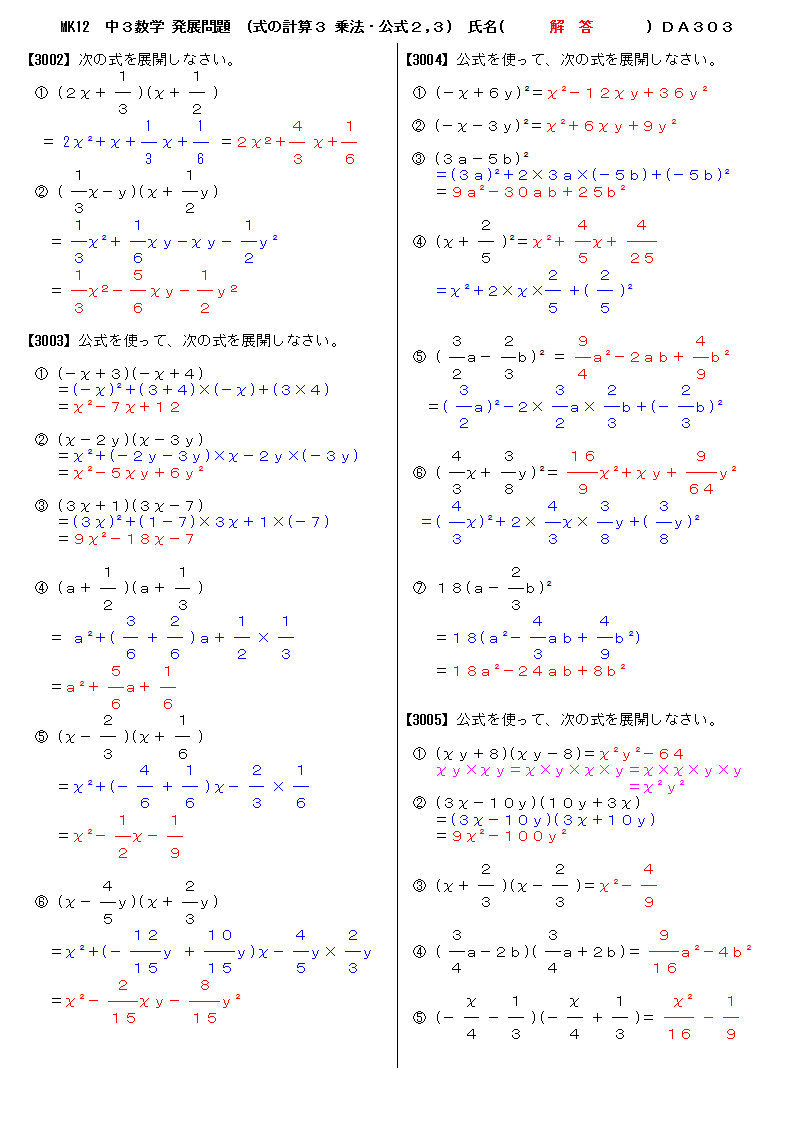中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	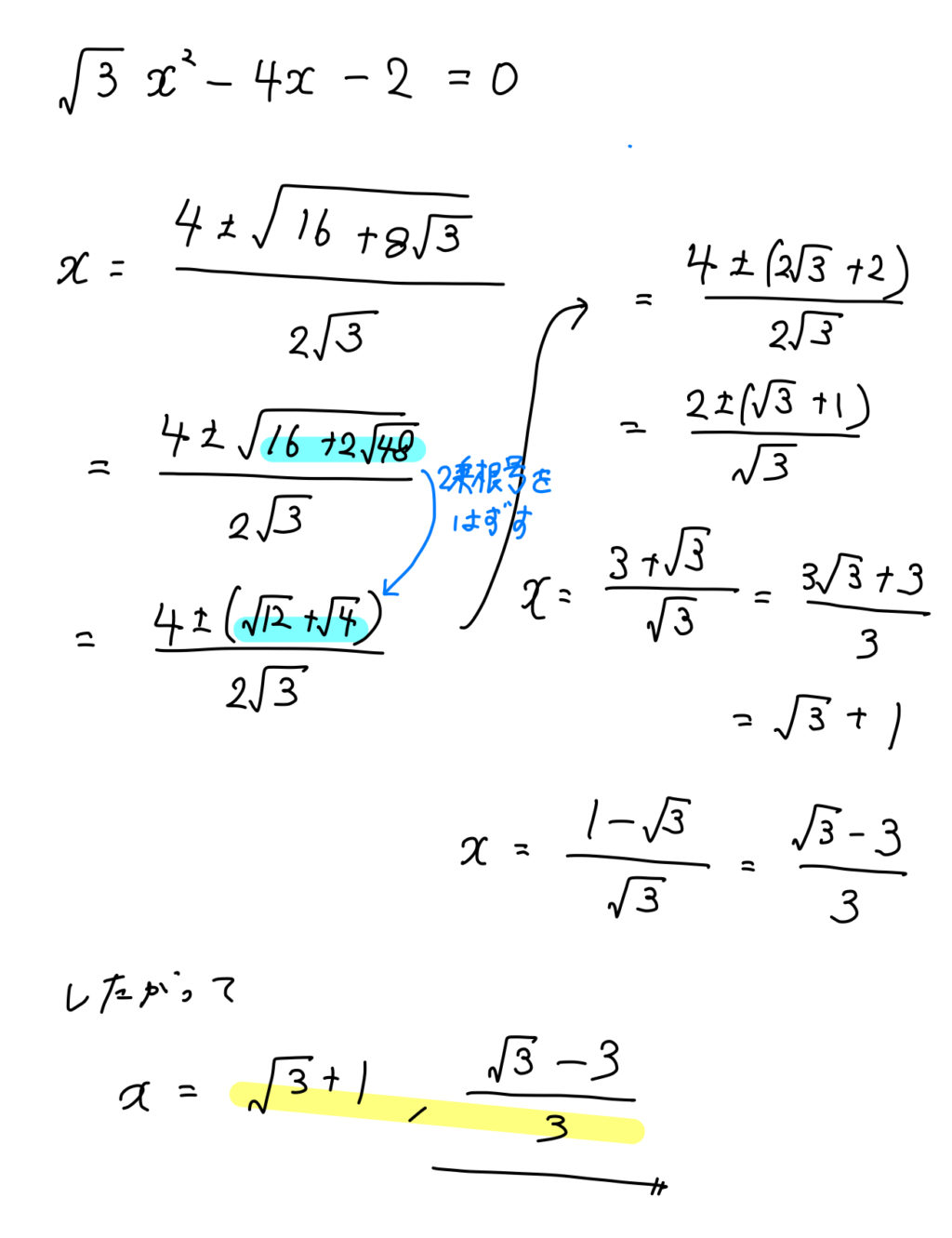中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
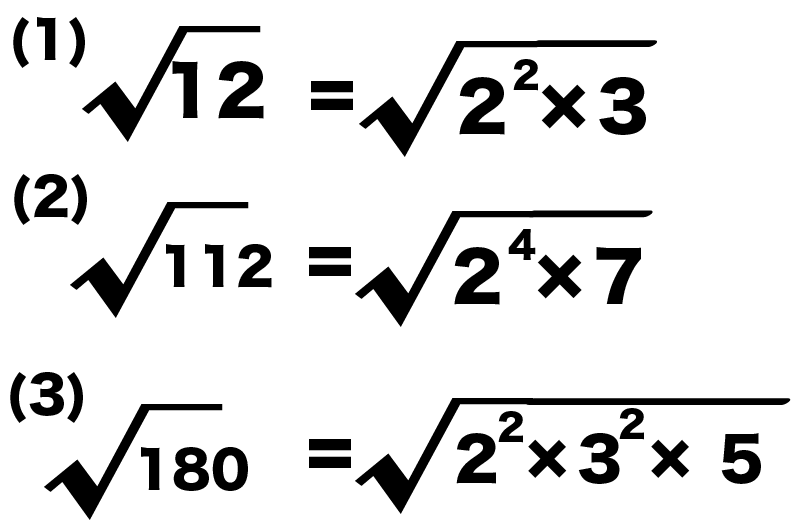中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	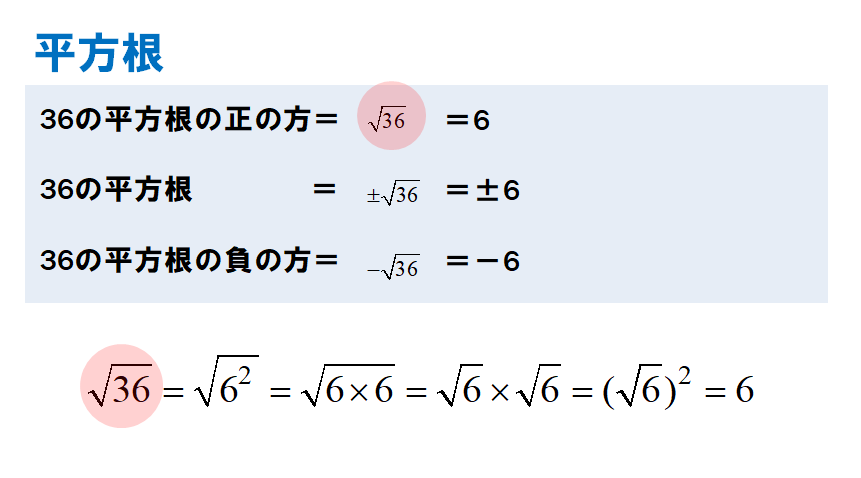中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に	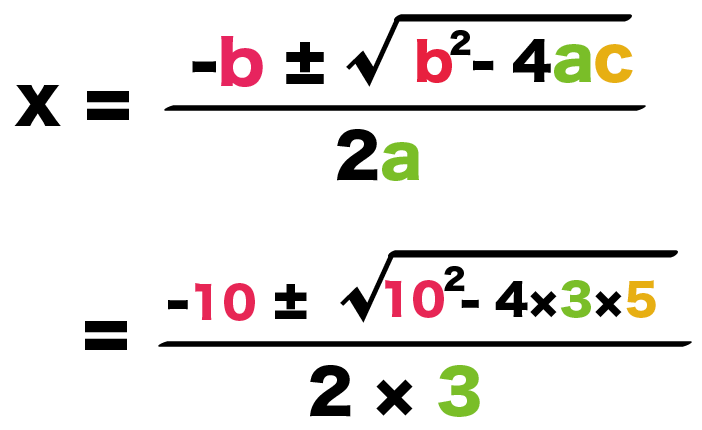中３ 平方根５ 有理数と無理数 中学数学の勉強に
中３ 平方根５ 有理数と無理数 中学数学の勉強に	中３ 平方根５ 有理数と無理数 中学数学の勉強に

 だから、ルートの中身を2乗の掛け算にすると、ルートが外せるよ 入試問題🈩(6)では、ルートの定義がわかっていないと解けないような問題が出題されるので、ここはしっかり覚えておいてね 具体的には、 $\sqrt{9} = \sqrt{3^2} = 3$ Mrシロ 今回は平方根の問題として紹介しましたが、「 を平方 (2乗)して整数になるnを求めよ！ 」のときも同じ方法で答えられます！ ただ「3乗して」のときはダメなので注意が必要です。 自然数とは 自然数は数の一種で、正の整数のことです。 ただ